2023年07月01日成考高起点每日一练《数学(理)》
成考高起点 2023-07-01作者:匿名 来源:本站整理
2023年成考高起点每日一练《数学(理)》7月1日专为备考2023年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知偶函数y=f(x),在区间[a,b](0 答 案:B 解 析:由偶函数的性质:偶函数在[a,b]和[-b,-a]上有相反的单调性,可知,y=f(x)在区间[a,b](0 2、如果不共线的向量a和b有相等的长度,则(a+b)(a-b)=()
答 案:A 解 析:(a+b)(a-b)= 3、过点(-2,2)与直线x+3y-5=0平行的直线是() 答 案:A 解 析:所求直线与x+3y-5=0平行,可设所求直线为x+3y+c=0,将点(一2,2)带入直线方程,故-2+3×2+c=0,解得c=-4,因此所求直线为线为x+3y-4=0. 4、已知全集U=R,A={x|x≥1},B={x|-1 答 案:A 解 析:补集运算应明确知道是否包括端点.A在U中的补集是x<1, 主观题 1、设函数f(x)= 答 案:(Ⅰ)函数的定义域为 2、在正四棱柱ABCD-A'B'C'D'中, 答 案:(Ⅰ)由题意知(如图所示) 3、已知数列 答 案: 4、已知a,b,c成等差数列,a,b,c+1成等比数列.若b=6,求a和c. 答 案:由已知得 填空题 1、不等式 答 案: 解 析: 2、设离散型随机变量 答 案:5.48 解 析: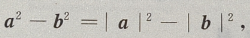
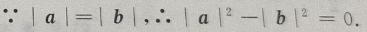



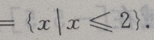
 (Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值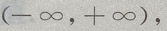
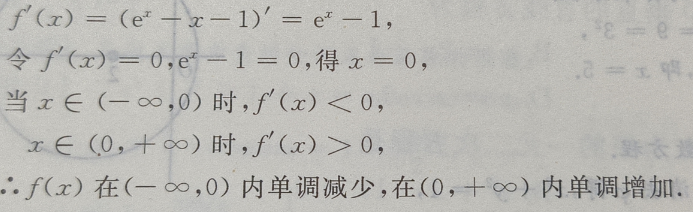 (Ⅱ)
(Ⅱ)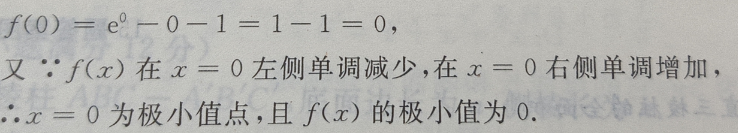
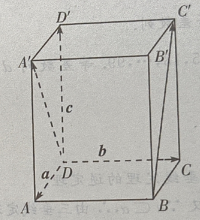
 (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
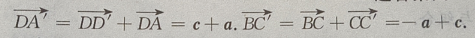
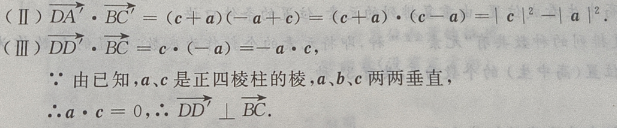
 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。


 解得
解得
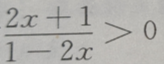 的解集为()
的解集为()
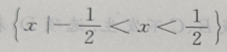


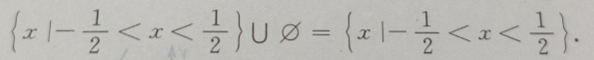
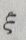 的分布列如下表,那么
的分布列如下表,那么 的期望等于()
的期望等于()

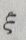 =6×0.7+5.4×0.1+5×0.1+4×0.06+0×0.04=5.48
=6×0.7+5.4×0.1+5×0.1+4×0.06+0×0.04=5.48