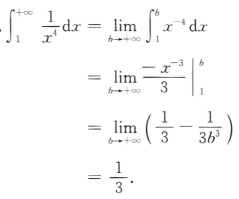2024年04月18日成考专升本每日一练《高等数学二》
成考(专升本) 2024-04-18作者:匿名 来源:本站整理
2024年成考专升本每日一练《高等数学二》4月18日专为备考2024年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设函数z=x2y3,则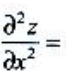 ().
().
- A:2y3
- B:6xy2
- C:6y2
- D:12xy
答 案:A
解 析: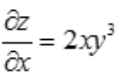 ,
,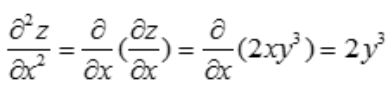 .
.
2、在x趋向于()时, 为无穷小量.
为无穷小量.
- A:2
- B:1
- C:-1
- D:+∞
答 案:D
解 析:A项,当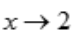 时,
时,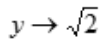 ;B项,当
;B项,当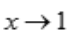 时,
时,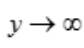 ;C项,由题意x≥0,且x≠1,故x不能趋向于-1;D项,当
;C项,由题意x≥0,且x≠1,故x不能趋向于-1;D项,当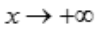 时,因为分子x的次幂小于分母中x的次幂,故
时,因为分子x的次幂小于分母中x的次幂,故 ,即为无穷小.
,即为无穷小.
主观题
1、证明:当x>0时,
答 案:证:令 ,
,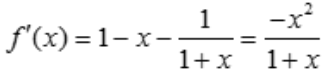 ,令
,令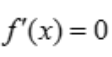 ,得x=0,f(0)=0,当x>0时,f'(x)<0,故函数单调递减,
,得x=0,f(0)=0,当x>0时,f'(x)<0,故函数单调递减,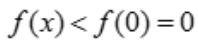 ,则
,则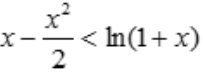 .令
.令 ,
,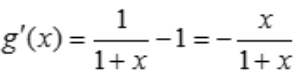 ,令
,令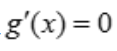 ,得x=0,g(0)=0,当x>0时,f'(x)<0,故函数单调递减,f(x)<f(0)=0,则
,得x=0,g(0)=0,当x>0时,f'(x)<0,故函数单调递减,f(x)<f(0)=0,则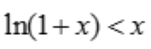 .综上得,当x>0时,
.综上得,当x>0时,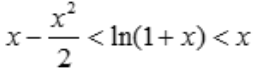 .
.
2、计算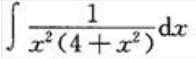 .
.
答 案:解: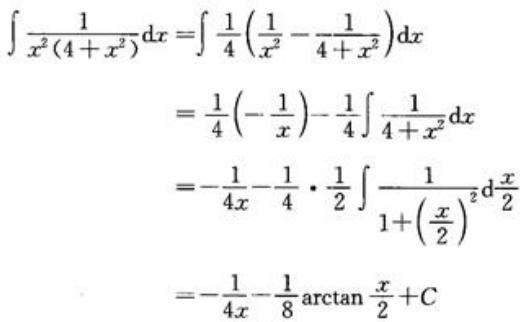
填空题
1、二元函数z=xy在x+y=1下的极值为()
答 案: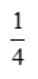
解 析:化为无条件极值,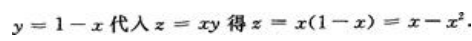 又因
又因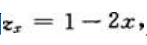 则令
则令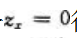 得驻点
得驻点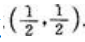 当
当 时,zx>0;当时zx<0,故该点
时,zx>0;当时zx<0,故该点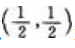 是极大值点且极大值
是极大值点且极大值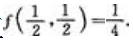
2、设随机变量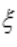 的分布列为
的分布列为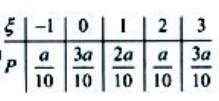 ,则a=().
,则a=().
答 案:1
解 析:因为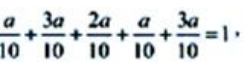 所以a=1.
所以a=1.
简答题
1、从一批有10件正品及2件次品的产品中,不放回地一件一件地抽取产品,设每个产品被抽到的可能性相同,求直到取出正品为止所需抽取的次数X的概率分布。
答 案:由题意,X的所有可能的取值为1,2,3, X=1,即第一次就取到正品,P{X=1}=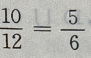 X=2,即第一次取到次品且第二次取到正品,P{X=2}=
X=2,即第一次取到次品且第二次取到正品,P{X=2}=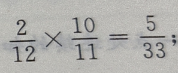 同理,P{X=3}=
同理,P{X=3}=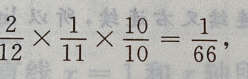 故X的概率分布如下
故X的概率分布如下
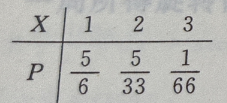
2、计算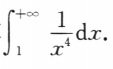
答 案: