2025年04月05日成考高起点每日一练《数学(理)》

2025年成考高起点每日一练《数学(理)》4月5日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知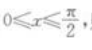则函数 y=sinx+cosx的值城为（）。

• A：[-1,1]
• B：
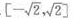
• C：
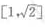
• D：

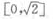
答 案：C

2、已知sinα=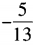，且540°＜α＜630°，则sin2α=（）。

• A：
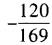
• B：
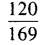
• C：
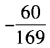
• D：

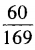
答 案：B

解 析：由已知，360°+180°＜α＜360°+270°，所以α是第三象限的角，故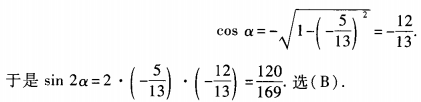

3、二项式(2x－1)⁶的展开式中，含x⁴项系数是（）。

• A：-15
• B：-240
• C：15
• D：240

答 案：D

解 析：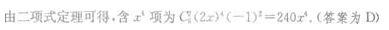

4、已知2^a=3，2^b=6，2^C=12，则（）.  

• A：b²=a+c
• B：2b=ac
• C：2b=a+c
• D：b²=ac

答 案：C

解 析：由已知，2^a·2^c=36，即2^a+c=36。又（2^b）²=6²，2^2b=36，则2^2b=2^a+c，2b=a+c选C。

主观题

1、已知x+x^-1=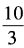，求x²+x-2的值。

答 案：由已知，得

2、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得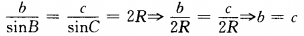

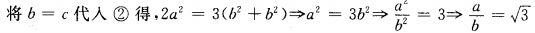
∴a：b=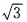：1
于是a：b：c=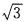：1：1。  

3、设分别讨论x→0及x→1时f（x）的极限是否存在？

答 案：∴f（x）在x=0处极限不存在 同理f（x）在x=1处极限存在

4、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得AB=120m,求河的宽

答 案：如图， ∵∠C=180°-30°-75°=75° ∴△ABC为等腰三角形，则AC=AB=120m 过C做CD⊥AB,则由Rt△ACD可求得CD==60m， 即河宽为60m  

填空题

1、y=cos²2x的最大值是______，最小值______，周期T=______。  

答 案：1；0；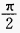

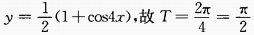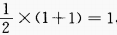解 析：，最大值为，最小值为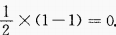

2、函数y=2cosx-cos2x（x∈R）的最大值为______。  

答 案：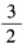

解 析：