2025年04月26日高职单招每日一练《数学(中职)》
高职单招 2025-04-26作者：匿名 来源：本站整理
2025年高职单招每日一练《数学(中职)》4月26日专为备考2025年数学(中职)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
单选题
1、抛物线x²=8y的准线方程为()
- A：x=-2
- B：y=-2
- C：x=2
- D：y=2
答 案：B
解 析：易知抛物线x2=8y的焦点在y轴正半轴上，且2p=8,即p=4,所以抛物线x2=8y的准线方程为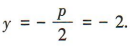
2、不等式lg(x-1)的定义域是( )
- A：{x|x＜0}
- B：{x|x＞1}
- C：{x|x∈R}
- D：{x|0＜x＜1}
答 案：B
3、若直线ax-y-2a-1=0与圆x²+y²-2x-1=0相切，则a的值是（）
- A：2
- B：
- C：1
- D：
答 案：C
解 析：由x²+y²-2x-1=0得(x-1)²+y²=2,则圆的圆心坐标为(1,0),半径为.由题意知圆心(1,0)到直线ax-y-2a-1=0的距离等于半径，即
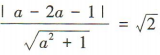整理得(a-1)²=0,解得a=1.
主观题
1、已知
答 案：方法一：矢量图表示法 矢量图表示法如图所示。
方法二：矢量表示法
解 析：
填空题
1、若函数f(x)=x2+2ax+3在区间[-4,6]上是单调函数，则实数a的取值范围（）
答 案：(-∞,-6]∪[4,+∞)
解 析：易得二次函数f(x)=x2+2ax+3的图像开口向上，对称轴为直线x=-a.因为f(x)在区间[-4,6]上是单调函数，所以
2、已知等差数列{an}的公差为d(d≠0),且a1,a3,a6成等比数列，则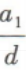
()
答 案：4
解 析：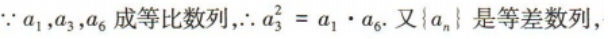
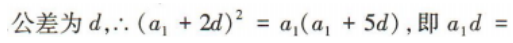
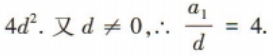
3、某机床生产一种零件,10天中,机床每天出的次品数分别是:0,1,0,2,2,0,3,1,2,4，则这10天中的次品数的中位数为()
答 案：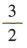
解 析：10天中的次品数由小到大排成一列为 0,0,0,1,1,2,2,2,3,4,所以这 10天中的次品数的中位数为
简答题
1、已知向量a=(1,x),b=(2x+3,-x). (1)若a//b,求|a-b|; (2)若a与b的夹角为锐角，求x的取值范围.
答 案：(1)因为a=(1,x),b=(2x+3,-x),a//b, 所以-x=x(2x+3),解得x=0或x=-2.
当x=0时，a=(1,0),b=(3,0),
所以a-b=(-2,0),
所以|a-b|=2;
当x=-2时，a=(1,-2),b=(-1,2),
所以a-b=(2,-4),
所以|a-b|=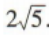
.
综上，|a-b|=2或Ia-bl=
.
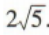(2)由a与b的夹角为锐角，得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1＜x＜3且x≠0,所以x的取值范围是(-1,0)∪(0,3).