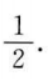2025年05月28日成考高起点每日一练《数学(文史)》

2025年成考高起点每日一练《数学(文史)》5月28日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、一批产品共有5件，其中4件为正品，1件为次品，从中一次取出2件均为正品的概率为（）。

• A：0.6
• B：0.5
• C：0.4
• D：0.3

答 案：A

解 析：本题主要考查的知识点为随机事件的概率。 一次取出2件均为正品的概率为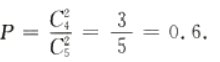

2、设成等比数列,则x等于  

• A：0或-2
• B：1或-1
• C：0或-2
• D：-2

答 案：C

解 析：由已知条件的得

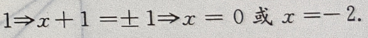
3、函数f（x）=sinx+x³（）。

• A：是偶函数
• B：是奇函数
• C：既是奇函数，又是偶函数
• D：既不是奇函数，又不是偶函数

答 案：B

4、不等式x²+x+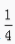＞0的解集是（）。

• A：不等于- 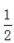的全体实数  
• B：全体实数集
• C：空集
• D：x≠ 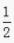的一切实数

答 案：A

主观题

1、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。  

答 案：由已知，得

2、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数.  

答 案：设每亩增种x棵,总收入味y元，则每亩种树(20+x)棵，由题意知增种x棵后每棵收入为（60-3x） 则有y=(90-3x)(20+x) 整理得y=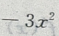+30x+1800 配方得y=+1875 当x=5时，y有最大值，所以每亩地最多种25棵

3、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

4、求函数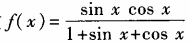（x∈R）的最大值与最小值。  

答 案：设sinx+cosx=t，则（sinx+cosx）²=t²，1+2sinxcosx=t²，sinxcosx= 于是转化为求的最值。 由所设知 上为增函数，故g（t）的最大值为最小值为

填空题

1、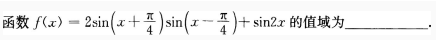  

答 案：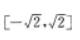

解 析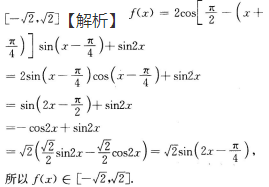： 【考点指要】本题主要考查三角函数的最大值、最小值及值域的求法，解题时需要灵活运用诱导公式、二倍角公式以及辅助角公式，当函数可以化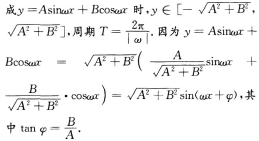

2、过点（2，0）作圆x2+y2=1的切线，切点的横坐标为（）。

答 案：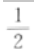

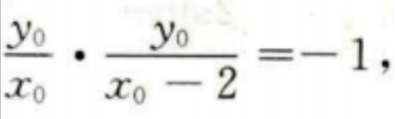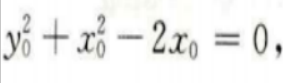
解 析：本题主要考查的知识点为圆的切线. 设切点(x0,y0)则有 即所以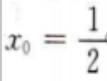故切点横坐标为