2025年05月28日高职单招每日一练《数学(中职)》
高职单招 2025-05-28作者:匿名 来源:本站整理
2025年高职单招每日一练《数学(中职)》5月28日专为备考2025年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、如果两个球的表面积的比值为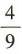 ,那么这两个球的体积的比值为()
,那么这两个球的体积的比值为()
- A:

- B:
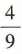
- C:

- D:

答 案:C
解 析:设两个球的半径分别为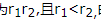 由题意得
由题意得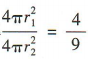 ,所以
,所以 ,所以两个球的体积的比值为
,所以两个球的体积的比值为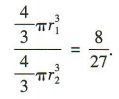
2、已知圆锥的底面半径为 2,高为  ,则其侧面积为()
,则其侧面积为()
- A:
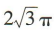
- B:4π
- C:6π
- D:8π
答 案:D
解 析:由圆锥的半径r= 2,高为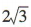 ,可得母线长
,可得母线长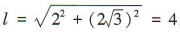 ,所以圆锥的侧面积S=mrl=πx2x4=8π.
,所以圆锥的侧面积S=mrl=πx2x4=8π.
3、若向量a=(2,-4),b=(2,1),则a+2b=()
- A:(4,-3)
- B:(4,0)
- C:(6,-3)
- D:(6,-2)
答 案:D
解 析:因为向量a=(2,-4),b=(2,1),所以a+2b=(2,-4)+2(2,1)=(6,-2).
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、已知椭圆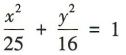 上一点 P到椭圆的一个焦点的距离为3,则 P到另一个焦点的距离为()
上一点 P到椭圆的一个焦点的距离为3,则 P到另一个焦点的距离为()
答 案:7
解 析:设F1,F2为椭圆的两个焦点,且|PF1|ㄧ=3.由题意知,椭圆的长半轴长a=5,则由椭圆定义知|PF2|=2a-|PF1|=2x5-3 = 7.
2、已知集合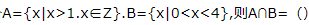
答 案:{2,3}
解 析: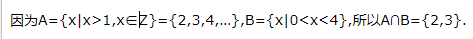
3、已知函数f(x)是R上的奇函数,且在(0,+∞)上单调递减,f(-5)=0,则不等式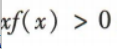 的解集是()
的解集是()
答 案:(-5,0)∪(0,5)
解 析:根据题意画出f(x)的大致图像如图所示.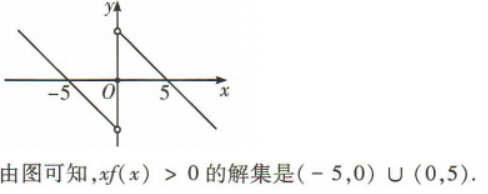
简答题
1、已知双曲线C的标准方程为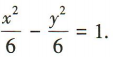 (1)求双曲线C的离心率,左、右焦点F1,F2的坐标;
(2)若点M(3,m)在双曲线C上,证明:
(1)求双曲线C的离心率,左、右焦点F1,F2的坐标;
(2)若点M(3,m)在双曲线C上,证明: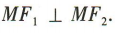
答 案:(1)由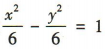 ,可得
,可得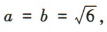 所以
所以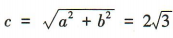 ,离心率
,离心率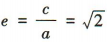 ,左、右焦点的坐标分别为
,左、右焦点的坐标分别为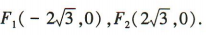 (2)因为点M(3,m)在双曲线C上,
所以
(2)因为点M(3,m)在双曲线C上,
所以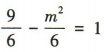 ,解得m2=3,
所以直线 MF1的斜率
,解得m2=3,
所以直线 MF1的斜率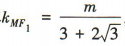 ,直线MF2的斜率
,直线MF2的斜率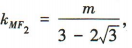 因为
因为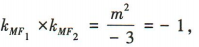 所以
所以